Background¶
Q-MM is Python toolbox to optimise objective functions like
where \(x\) is the unknown of size \(N\), \(V_k\) a matrix or linear operator of size \(M_k \times N\), \(\omega_k\) a data fixed vector of size \(M_k\), \(\mu_k\) a scalar hyperparameter, and \(\Psi_k(u) = \sum_i \varphi_k(u_i)\). Q-MM suppose that the scalar functions \(\varphi\) are differentiable, even, coercive, \(\varphi(\sqrt{\cdot})\) concave, and \(0 < \dot{\varphi}(u) / u < +\infty\).
The optimization is done thanks to quadratic surrogate function. In particular, no linesearch is necessary and close form formula for the step are used with guaranteed convergence. The explicit step formula allows fast convergence of the algorithm to a minimizer of the objective function without tuning parameters. On the contrary, the objective must meet the conditions above.
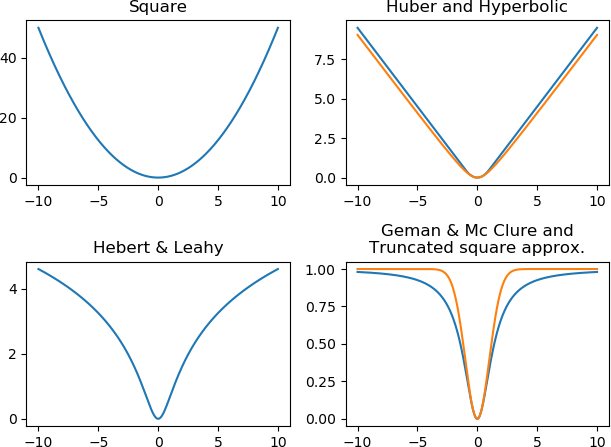
The losses implemented in the toolbox, in addition to the square function, are illustrated below. The Geman & Mc Clure and the truncated square approximation are not coercive.
Example¶
A classical example is the resolution of an inverse problem with the minimization of
where \(H\) is a low-pass forward model, \(V\) a regularization operator that approximate object gradient (kind of high-pass filter) and \(\Psi\) an edge preserving function like Huber. The above objective is obtained with \(k \in \{1, 2\}\), \(\Psi_1(\cdot) = \|\cdot\|_2^2\), \(V_1 = H\), \(\omega_1 = y\), and \(\omega_2 = 0\).
References¶
The toolbox is funded on following papers. The papers [a], [b], and [c] are historical foundations. The implemented algorithms in the toolbox come from [d] and [e]. If you use this toolbox please cite these last two papers and this toolbox as
@software{qmm,
title = {Q-MM: The Quadratic Majorize-Minimize Python toolbox},
author = {Orieux, Fran\c{c}ois},
url = {https://github.com/forieux/qmm},
}
- a
D. Geman and G. Reynolds, “Constrained restoration and the recovery of discontinuities,” IEEE Trans. Pattern Anal. Machine Intell., vol. 14, no. 3, pp. 367–383, Mar. 1992, doi: 10.1109/34.120331.
- b
D. Geman and C. Yang, “Nonlinear image recovery with half-quadratic regularization,” IEEE Trans. on Image Process., vol. 4, no. 7, pp. 932–946, Jul. 1995, doi: 10.1109/83.392335.
- c
M. Allain, J. Idier, and Y. Goussard, “On Global and Local Convergence of Half-Quadratic Algorithms,” IEEE Trans. on Image Processing, vol. 15, no. 5, p. 13, 2006.
- d
C. Labat and J. Idier, “Convergence of Conjugate Gradient Methods with a Closed-Form Stepsize Formula,” J Optim Theory Appl, p. 18, 2008.
- e
E. Chouzenoux, J. Idier, and S. Moussaoui, “A Majorize-Minimize Strategy for Subspace Optimization Applied to Image Restoration,” IEEE Trans. on Image Process., vol. 20, no. 6, pp. 1517–1528, Jun. 2011, doi: 10.1109/TIP.2010.2103083.